Grafici sul piano cartesiano

L'angolo di Susan: la tecnologia per la matematica

Come insegnare a uno studente cieco a tracciare un grafico su un piano delle coordinate: senza tecnologia, con strumenti a basso livello tecnologico, con strumenti ad alto livello tecnologico

Premessa

Anche se l'utilizzo delle calcolatrici scientifiche per i grafici è ora uno strumento essenziale in una classe di matematica alla scuola secondaria, tutti gli studenti dovrebbero dapprima comprendere il concetto di come tracciare manualmente un grafico su un piano delle coordinate. Io insisto moltissimo sul fatto che i miei studenti siano in grado di tracciare fisicamente i punti e le linee del grafico, come pure di ricavarne la curva. Questa capacità è ancora più importante per gli studenti ciechi, dal momento che essi non hanno accesso alla maggior parte degli strumenti tecnologici per la matematica.

Il Problema

Recentemente ho ricevuto una valanga di richiesta di aiuto da parte di insegnanti di sostegno di studenti ciechi e di insegnanti di matematica. Domanda: "Come possono gli studenti ciechi tracciare il grafico delle equazioni lineari, delle disuguaglianze e dei sistemi delle disuguaglianze in maniera indipendente ed efficiente? Oppure è un argomento che questi studenti non possono affrontare a causa della sua natura visiva?". Risposta: La maggior parte degli universitari ciechi, anche quelli con problemi di orientamento nello spazio, è sicuramente in grado di tracciare grafici e, come ha detto uno dei miei studenti, "Non solo possiamo farlo, è anche divertente!".

Soluzioni senza tecnologia, con strumenti a basso livello tecnologico e ad alto livello tecnologico

L'Ausilio Grafico per la Matematica della APH è validissimo per tracciare i grafici delle equazioni algebriche ma può essere utilizzato anche nella geometria, nella trigonometria, ecc. Consiste in una lastra di sughero montata su una base di gomma, su cui è stata intessuta una griglia di quadrati i cui lati misurano ½ pollice ( 1,27 cm). I miei studenti utilizzano due bande perpendicolari in gomma, bloccate con puntine da disegno, per gli assi x ed y. Poi tracciano i punti sulle relative coordinate utilizzando spilli a capocchia. Questi punti vengono collegati con strisce di gomma (per le linee), con sezioni piatte di molle (per le sezioni coniche) o con cordicelle (per le funzioni dei polinomi). Gli insegnanti vedenti di matematica sono in grado di interpretare correttamente e con facilità i grafici realizzati dagli studenti. Lo studente può anche costruirsi una sua tavola di gomma per i grafici attaccando un foglio di carta millimetrata a rilievo (anch'essa fornita dalla APH) ad una lastra di sughero e procedere come sopra descritto.

Vorrei ricordare anche l'uso dei Wikki Stix (fili di tessuto ricoperti di cera) e dei punti a rilievo sulla carta millimetrata APH quando lo studente DEVE consegnare una copia dei grafici assegnati come compito a casa ad insegnanti di matematica particolarmente esigenti. Però questo metodo può essere molto costoso, richiede un notevole dispendio di tempo ed è più che altro un test delle capacità artistiche. Io desidero DAVVERO che i miei studenti realizzino parecchi grafici, e loro possono farlo in maniera incredibilmente veloce utilizzando l'Ausilio Grafico per la Matematica della APH. In effetti, molti dei miei studenti vedenti insistono per usarlo anche loro, dal momento che è più rapido, è divertente e consente di imparare a realizzare grafici con una modalità diversa.

Oltre a questo ausilio, i miei studenti utilizzano la calcolatrice scientifica parlante ORION TI-34 della Orbit Research, che consente loro di effettuare tutti i calcoli necessari ad accelerare la procedura di realizzazione del grafico.

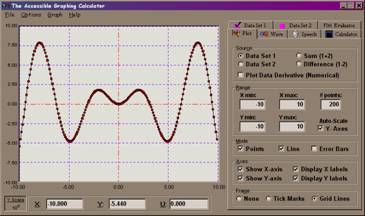
Quando iniziamo ad esplorare le equazioni lineari, io presento la AGC (Accessible Graphing Calculator, Calcolatrice Accessibile per i Grafici, della ViewPlus Technologies). Ad esempio, il nostro libro di testo presenta un problema esplorativo, dove gli studenti devono dapprima stabilire se il grafico di una data equazione risulterà in una linea retta o no; dopo di che, dovranno verificare la correttezza della loro ipotesi realizzando questo grafico. Il testo elenca circa 10 equazioni: beh, ci vorrebbe davvero parecchio tempo se gli studenti dovessero calcolare tutto manualmente, tanto più che la maggior parte di loro non conosce ancora le equazioni di secondo grado e le funzioni razionali. Tuttavia, queste equazioni possono essere rapidamente inserite nella calcolatrice AGC e gli studenti possono ascoltare l'emissione sonora e conoscere immediatamente le differenze tra y=3*x+4, y=x^2, e y=3/x+2 (il modo in cui bisogna inserire le equazioni nella calcolatrice AGC). Inoltre, abbiamo collegato una stampante TIGER Advantage (stampante che consente la produzione di grafici a rilievo) ad ogni computer, così i miei studenti riescono anche a realizzare ogni grafico in modo estremamente rapido.

Il mio orgoglio e la mia gioia è uno studente che utilizza il Braille e che ho avuto l'anno scorso nella prima classe di algebra. Gli ho insegnato come realizzare manualmente i grafici e poi gli ho mostrato l'uso della calcolatrice AGC, che ho spiegato più sopra. Ora si trova nella seconda classe di algebra e lavora bene con entrambi i metodi. Io continuo a mostrargli come risolvere i problemi della seconda classe di algebra, sia manualmente che utilizzando la tecnologia, e lui stabilisce il metodo più adatto a seconda delle diverse circostanze. Ad esempio, a volte realizza manualmente il grafico di una funzione di secondo grado perché "era troppo facile per disturbarsi ad usare il computer"; invece utilizza la calcolatrice AGC per realizzare il grafico di una funzione esponenziale.

Problemi specifici

Come fanno gli studenti a rappresentare le disuguaglianze che sul grafico si esprimono con una linea continua o con una linea tratteggiata?

Ripeto: i miei studenti utilizzano l'Ausilio Grafico per la Matematica della APH (che ha una griglia in rilievo), strisce di gomma bloccate da puntine da disegno per creare gli assi x e y e spilli a capocchia per tracciare i punti. Colleghiamo poi questi punti per mezzo di una striscia di gomma quando la linea di contorno (la linea continua, nei grafici a stampa) deve essere inserita nella soluzione, mentre non utilizziamo la striscia di gomma quando la linea di contorno non deve essere inserita nella soluzione (nei grafici a stampa è la linea tratteggiata).

Come fanno a mostrare le parti ombreggiate del grafico?

Quando si realizza il grafico di una disuguaglianza in due variabili, i miei studenti appoggiano semplicemente la mano sulla parte ombreggiata. Quando realizzano il grafico di un sistema di due disuguaglianze, gli studenti appoggiano una mano sulla parte ombreggiata della prima disuguaglianza, poi appoggiano l'altra mano sulla parte ombreggiata della seconda disuguaglianza. Il punto in cui le due mani si sovrappongono (comprese le linee di contorno, là dove esistono) costituisce la soluzione. Ben presto la maggior parte dei miei studenti è in grado di esaminare tre o più disuguaglianze senza una molteplice sovrapposizione delle mani. Arriviamo persino ad affrontare problemi di programmazione lineare comprendenti quattro o più disuguaglianze: in questi problemi, spesso si incontra un'area limitata con vertici ed a questo punto è facilissimo individuare la zona ombreggiata (cioè la soluzione).

3. Esiste un sistema con cui gli studenti ciechi possono risolvere problemi multipli su un foglio di carta?

Io controllo ogni singolo grafico, man mano che i miei studenti li completano. Ad esempio, durante un test, mi hanno fatto controllare ogni singolo grafico e scrivere una nota sul loro foglio di carta prima di passare al problema successivo. Io controllo se le linee di contorno sono state realizzate correttamente (con o senza strisce di gomma) e se gli studenti hanno collocato l'"ombreggiatura" al posto giusto.

Se lo studente deve consegnare un certo numero di grafici, suggerisco di utilizzare questa procedura:

Se deve tracciare un grafico su un piano delle coordinate, lo studente può utilizzare la carta millimetrata a rilievo della APH, attaccandola ad una tavola di sughero. Poi, potrebbe tracciare i punti servendosi di adesivi a rilievo, vernice gonfiabile ecc. Per creare le linee continue può utilizzare i Wikki Stix, fili di tessuto ricoperti di cera. Può servirsi anche di una penna o di una matita colorata, oppure di un pastello, per colorare l'area ombreggiata della soluzione. Naturalmente, tutto ciò richiede tempi MOLTO più lunghi rispetto al nostro metodo, ma potrebbe rivelarsi necessario se allo studente viene chiesto di consegnare una copia cartacea del grafico, realizzata a mano. Inoltre, lo studente potrebbe realizzare facilmente una copia cartacea di ogni singola funzione (non è possibile realizzare un unico grafico per le funzioni multiple), creata con la calcolatrice AGC.

Una volta ho avuto una studentessa il cui insegnante di matematica insisteva sul fatto che ogni grafico doveva essere presentato sui due lati di un foglio di carta, ognuno contenente nove piccoli piani delle coordinate. Questa studentessa ha realizzato il grafico di ogni equazione sulla sua tavola dei grafici ed io ho copiato il suo lavoro sul foglio di carta "prestabilito". La studentessa era scocciata perché non riuscivo a reggere il suo ritmo e rallentavo il suo lavoro! Ciò nonostante, è stata promossa con ottimi voti.

Preferisco che gli studenti imparino ad utilizzare in maniera efficace la tavola in gomma per i grafici, dato che con questo metodo imparano MOLTO DI PIU', ed oltre tutto in maniera indipendente. Come alternativa, si può dividere l'Ausilio Grafico per la Matematica della APH in 4 o 6 diversi piani delle coordinate, di piccole dimensioni. Se si possiede una fotocamera digitale, i grafici realizzati dagli studenti possono persino essere inviati via e-mail o stampati! Meglio ancora: lasciate che sia lo studente a scattare la foto, oppure i suoi genitori!

Conclusioni

E' IMPORTANTE che tutti i vostri studenti possano partecipare a tutti i tipi di realizzazione di grafici e che abbiano a disposizione gli strumenti adeguati. Questa esplorazione creativa dovrebbe iniziare dalle classi inferiori ed avere il tempo sufficiente a maturare. Ricordate che la bellezza di un grafico tattile si trova sulla punta delle dita di chi lo esamina e che non esiste un grafico più bello e più significativo di quello creato da quelle stesse dita.